The SURG regularly publishes its findings in scientific journals. We publish in a wide-range of disciplines. Examples of these publications, grouped by broad disciplines, can be found below (click the arrows under each topic to expand the publication list). For a complete list of publications, see Prof. Shields’ Google Scholar Page.
Scientific Machine Learning
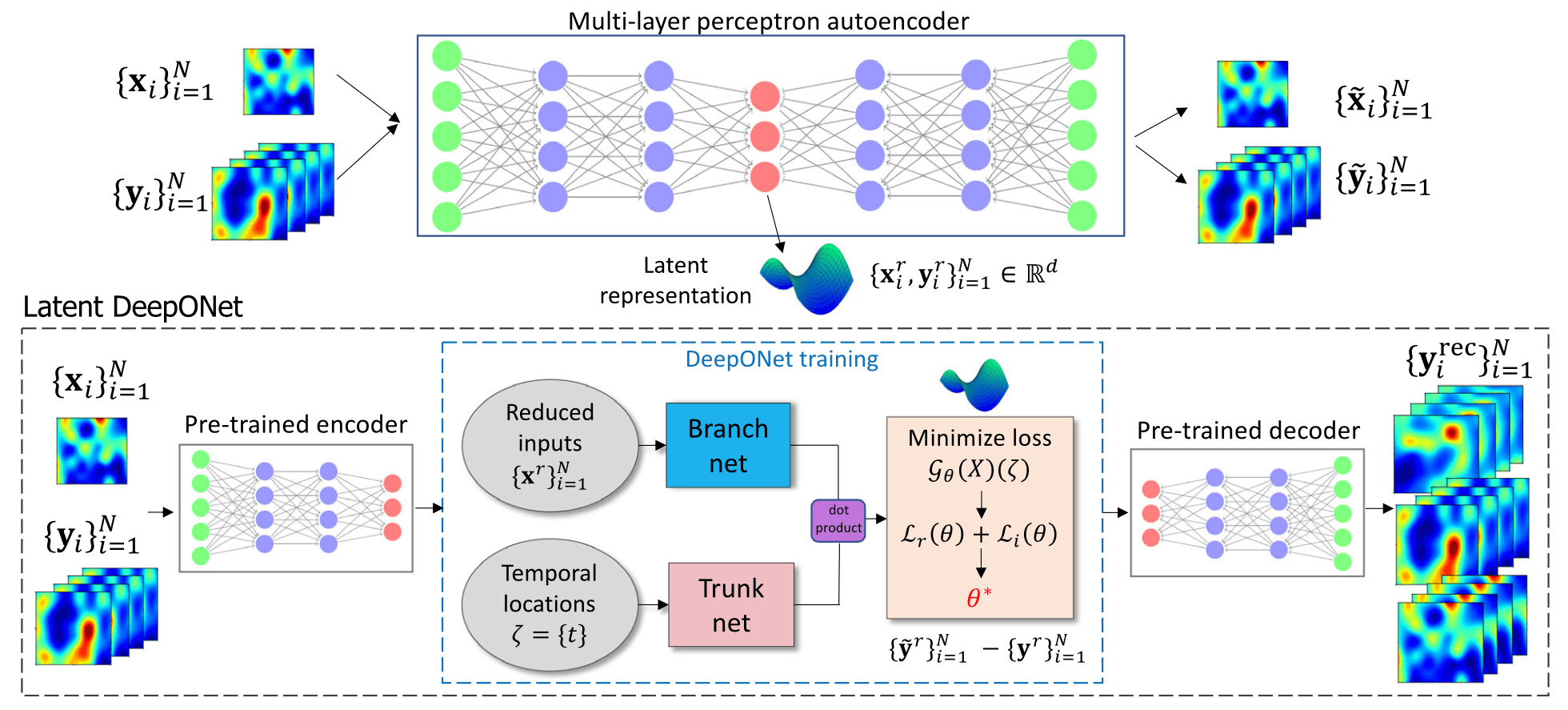
The field of Scientific Machine Learning (SciML) has emerged in the past decade to use modern machine learning (ML) tools to solve problems in the sciences. Very often this involves using ML methods to solve physical systems governed by partial differential equations. In SURG, we are developing SciML methods for surrogate modeling in UQ and building new SciML methods with quantified uncertainty to assess confidence in their predictive power. The following are representative papers:
- B. Bahmani, S. Goswami, I. G. Kevrekidis, and M. D. Shields. “A Resolution Independent Neural Operator”. Computer Methods in Applied Mechanics and Engineering. 444 (2025), p. 118113. [DOI].
- G.D. Pasparakis, L. Graham-Brady, and M. D. Shields. “Bayesian neural networks for predicting uncertainty in full-field material response”. Computer Methods in Applied Mechanics and Engineering. 433 (2025), p. 117486. [DOI]
- V. Kumar, S. Goswami, K. Kontolati, G. E. Karniadakis, and M. D. Shields. “Synergistic Learning with Multi-Task DeepONet for Efficient PDE Problem Solving”. Neural Networks. 184 (2025), p. 107113. [DOI]
- H. Sharma, L. Novak, and M. D. Shields. “Physics-Constrained Polynomial Chaos Expansion for Scientific Machine Learning and Uncertainty Quantification”. Computer Methods in Applied Mechanics and Engineering. 431 (2024), p. 117314. [DOI]
- K. Kontolati, S. Goswami, G. E. Karniadakis, and M. D. Shields. “Learning nonlinear operators in latent spaces for real-time predictions of complex dynamics in physical systems”. Nature Communications. 15 (2024), p. 5101. [DOI]
- K. Kontolati, S. Goswami, M. D. Shields, and G. Karniadakis. “On the influence of over-parameterization in manifold based surrogates and deep neural operators”. Journal of Computational Physics. 479 (2023), p. 112008. [DOI]
- M. D. Shields, K. Gurley, R. Catarelli, M. Chauhan, M. Ojeda-Tuz, and F. J. Masters. “Active Learning Applied to Automated Physical Systems Increases the Rate of Discovery”. Scientific Reports. 13 (2023), p. 8402. [DOI]
- K.R.M. dos Santos, D.G. Giovanis, and M. D. Shields. “Grassmannian diffusion maps-based dimension reduction and classification for high-dimensional data”. SIAM Journal on Scientific Computing. 44.2 (2022), B250–B274. [DOI]
- S. Goswami, K. Kontolati, M. D. Shields, and G. E. Karniadakis. “Deep transfer learning for partial differential equations under conditional shift with DeepONet”. Nature Machine Intelligence (2022). [DOI]
- K. Kontolati, D. Loukrezis, D.G. Giovanis, L. Vandanapu, and M. D. Shields. “A survey of unsupervised learning methods for high-dimensional uncertainty quantification in black-box-type problems”. Journal of Computational Physics 464 (2022), p. 111313. [DOI]
- A. Olivier, M. D. Shields, and L. Graham-Brady. “Bayesian neural networks for uncertainty quantification in data-driven materials modeling”. Computer Methods in Applied Mechanics and Engineering. 386 (2021), p. 114079. [DOI]
Structural Safety and Reliability

Assessing failure of critical engineering systems – such as buildings, bridges, aircraft, and nuclear reactors – is an incredibly difficult task with significant consequences. Challenges arise because these systems involve very large uncertainties, unknown or unpredictable failure modes, and system complexities that are high dimensional and nonlinear involving many interacting components. We develop statistical, mathematical, and computational methods to assess failure probabilities and uncertainty estimates in failure probabilities, particularly when models for the system are expensive, complex, and uncertain. The following are representative publications.
- P. Chakroborty, S. Dhulipala, and M. D. Shields. “Covariance-free Bi-fidelity Control Variates Importance Sampling for Rare Event Reliability Analysis”. SIAM Journal on Uncertainty Quantification (Accepted). [Arxiv]
- D. Thaler, S. Dhulipala, F. Bamer, B. Markert, and M. D. Shields. “Reliability Analysis of Complex Systems using Subset Simulations with Hamiltonian Neural Networks”. Structural Safety. 109 (2024), p. 102475. [DOI]
- P. Chakroborty, S. L. Dhulipala, Y. Che, W. Jiang, B. W. Spencer, J. D. Hales, and M. D. Shields. “General multi-fidelity surrogate models: Framework and active learning strategies for efficient rare event simulation”. Journal of Engineering Mechanics (2023). [DOI]
- D.G. Giovanis and M. D. Shields. “Imprecise Subset Simulation”. Probabilistic Engineering Mechanics. 66 (2022), p. 103293. [DOI]
- S. L. N. Dhulipala, M. D. Shields, P. Chakroborty, W. Jiang, B. W. Spencer, J. D. Hales, A. E. Slaughter, L. V. M., and C. Bolisetti. “Reliability Estimation of an Advanced Nuclear Fuel using Coupled Active Learning, Multifidelity Modeling, and Subset Simulation”. Reliability Engineering and System Safety. 226 (2022), p. 108693. [DOI]
- S. L. N. Dhulipala, M. D. Shields, B. W. Spencer, C. Bolisetti, A. E. Slaughter, L.V.M., and P. Chakroborty. “Active Learning with Multifidelity Modeling for Efficient Rare Event Simulation”. Journal of Computational Physics. 468 (2022), p. 111506. [DOI]
- M. D. Shields, D.G. Giovanis, and V.S. Sundar. “Subset Simulation for problems with strongly non-Gaussian, highly anisotropic, and degenerate distributions”. Computers & Structures 245 (2021), p. 106431. [DOI]
- V. S. Sundar and M. D. Shields. “Reliability analysis using adaptive Kriging surrogates with multimodel inference”. ASCE-ASME Journal of Uncertainty and Risk in Engineering Systems: Part A Civil Engineering. 5 (2019), p. 04019004. [DOI]
- V. S. Sundar and M. D. Shields. “Surrogate-enhanced stochastic search algorithms to identify implicitly defined functions for reliability analysis”. Structural Safety. 62 (2016), pp. 1–11. [DOI]
Uncertainty Quantification and Propagation
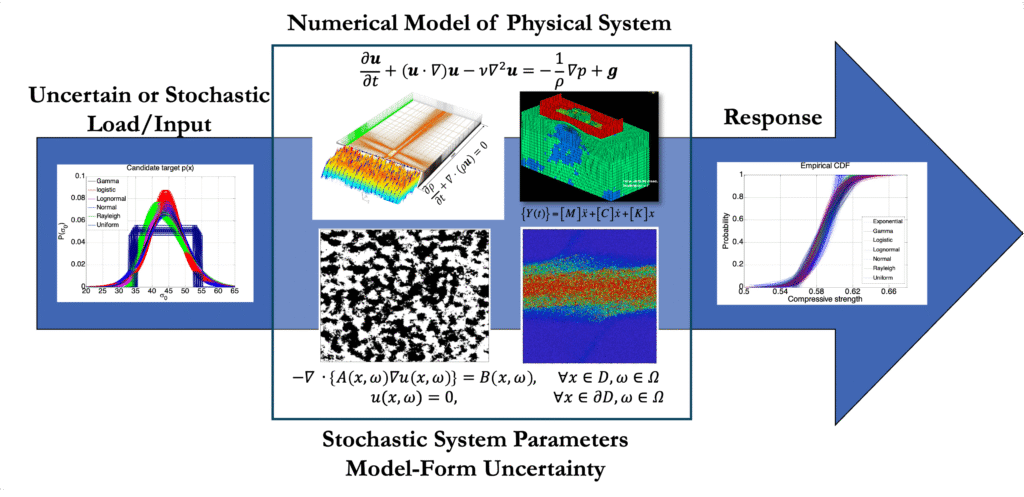
Engineering systems are rife with uncertainty. These uncertainties stem from sources ranging from the stochastic nature of many systems and their loading/excitation to assumptions made in the modeling and analysis of the system. These uncertainties can have huge implications for the system, its operation, and its safety. Therefore, it is critical that we quantify them and understand these impacts. In SURG, we develop probabilistic methods to quantify uncertainty and propagate them through engineering systems to assess their impacts. This includes developing novel Monte Carlo methods, surrogate models, global sensitivity analysis, Bayesian inference methods, and other techniques. The following are representative papers:
- D.G. Giovanis, D. Loukrezis, Y. Kevrekidis, and M. D. Shields. “Polynomial Chaos Expansions on Principal Geodesic Grassmannian Submanifolds for Surrogate Modeling and Uncertainty Quantification”. Journal of Computational Physics 519 (2024), p. 113443. [DOI]
- L. Novak, H. Sharma, and M. D. Shields. “Physics-informed Polynomial Chaos Expansions”. Journal of Computational Physics. 506 (2024), p. 112926. [DOI]
- M. Chauhan, M. Ojeda-Tuz, R. Catarelli, K. Gurley, D. Tsapetis, and M. D. Shields. “On active learning for Gaussian process-based global sensitivity analysis”. Reliability Engineering and Systems Safety. 245 (2024), p. 109945. [DOI]
- S. L. Dhulipala, Y. Che, and M. D. Shields. “Efficient Bayesian Inference with Latent Hamiltonian Neural Networks in No-U-Turn Sampling”. Journal of Computational Physics. 492 (2023), p. 112425. [DOI]
- L. Novak, M. D. Shields, V. Sadılek, and M. Vorechovsk. “Active Learning-based Domain Adaptive Localized Polynomial Chaos Expansion”. Mechanical Systems and Signal Processing. 204 (2023), p. 110728. [DOI]
- K.R.M. dos Santos, D.G. Giovanis, K. Kontolati, D. Loukrezis, and M. D. Shields. “Grassmannian diffusion maps based surrogate modeling via geometric harmonics”. Interntional Journal for Numerical Methods in Engineering. 563 (2022), pp. 1–23. [DOI]
- K. Kontolati, D. Loukrezis, K.R.M. dos Santos, D.G. Giovanis, and M. D. Shields. “Manifold learning-based polynomial chaos expansions for high-dimensional surrogate models”. Interntional Journal for Uncertainty Quantification. 12 (2022), pp. 39–64. [DOI]
- L. Novak, M. Vorechovsk, V. Sadılek, and M. D. Shields. “Variance-based adaptive sequential sampling for Polynomial Chaos Expansion”. Computer Methods in Applied Mechanics and Engineering. 386 (2021), p. 114105. [DOI]
- G. Banyay, M. D. Shields, and J. C. Brigham. “Efficient Global Sensitivity Analysis of Structural Vibration for a Nuclear Reactor System Subject to Nonstationary Loading”. Nuclear Engineering and Design. 361 (2020), p. 110544. [DOI]
- A. Bhaduri, D. Brandyberry, M. D. Shields, P. Geubelle, and L. Graham-Brady. “On the usefulness of gradient information in surrogate modeling: Application to uncertainty propagation in composite material models”. Probabilistic Engineering Mechanics. 60 (2020), p. 103024. [DOI]
- D.G. Giovanis and M. D. Shields. “Data-driven surrogates for high dimensional models using Gaussian process regression on the Grassmann manifold”. Computer Methods in Applied Mechanics and Engineering 370 (2020), p. 113269. [DOI]
- J. Zhang and M. D. Shields. “On the quantification and efficient propagation of imprecise probabilities with copula dependence”. International Journal of Approximate Reasoning. 122 (2020), pp. 24–46. [DOI]
- J. Zhang, S. Termaath, and M. D. Shields. “Imprecise global sensitivity analysis using Bayesian multimodel inference and importance sampling”. Mechanical Systems and Signal Processing. 148 (2020), p. 107162. [DOI]
- D. G. Giovanis and M. D. Shields. “Variance-based simplex stochastic collocation with model order reduction for high-dimensional response”. International Journal for Numerical Methods in Engineering. 117 (2019), pp. 1079–1116. [DOI]
- J. Zhang and M. D. Shields. “Efficient Monte Carlo resampling for probability measure changes from Bayesian updating”. Probabilistic Engineering Mechanics. 55 (2019), pp. 54–66. [DOI]
- A. Bhaduri, Y. He, M. D. Shields, L. Graham-Brady, and M. Kirby. “Stochastic collocation with adaptive mesh refinement for parametric uncertainty analysis”. Journal of Computational Physics. 371 (2018), pp. 732–750. [DOI]
- D. G. Giovanis and M. D. Shields. “Uncertainty quantification for complex systems with very high dimensional response using Grassmann manifold variations”. Journal of Computational Physics. 364 (2018), pp. 393–415. [DOI]
- K. Nahshon, N. Reynolds, and M. D. Shields. “Efficient uncertainty propagation for high-fidelity simulations with large parameter spaces: Application to stiffened plate buckling”. ASME Journal of Verification, Validation, and Uncertainty Quantification. 3 (2018), p. 011003. [DOI]
- J. Zhang and M. D. Shields. “On the quantification and propagation of imprecise probabilities resulting from small datasets”. Mechanical Systems and Signal Processing. 98 (2018), pp. 465–483. [DOI]
- J. Zhang and M. D. Shields. “The effect of prior probabilities on quantification and propagation of imprecise probabilities resulting from small datasets”. Computer Methods in Applied Mechanics and Engineering. 334 (2018), pp. 483–506. [DOI]
- M. D. Shields. “Adaptive Monte Carlo analysis for strongly nonlinear stochastic systems”. Reliability Engineering and System Safety. 175 (2018), pp. 207–224. [DOI]
- M. D. Shields. “Refined Latinized Stratified Sampling: A robust sequential sample size extension methodology for high-dimensional Latin hypercube and stratified designs”. International Journal for Uncertainty Quantification. 6.1 (2016), pp. 79–97. [DOI]
- M. D. Shields and J. Zhang. “The generalization of Latin hypercube sampling”. Reliability Engineering & System Safety. 148 (2016), pp. 96–108. [DOI]
- M. D. Shields, K. Teferra, A. Hapij, and R. P. Daddazio. “Refined Stratified Sampling for efficient Monte Carlo based uncertainty quantification”. Reliability Engineering & System Safety. 142 (2015), pp. 310–325. [DOI]
- K. Teferra, M. D. Shields, A. Hapij, and R. P. Daddazio. “Mapping model validation metrics to subject matter expert scores for model adequacy assessment”. Reliability Engineering & System Safety. 132 (2014), pp. 9–19. [DOI]
Natural Hazards Modeling
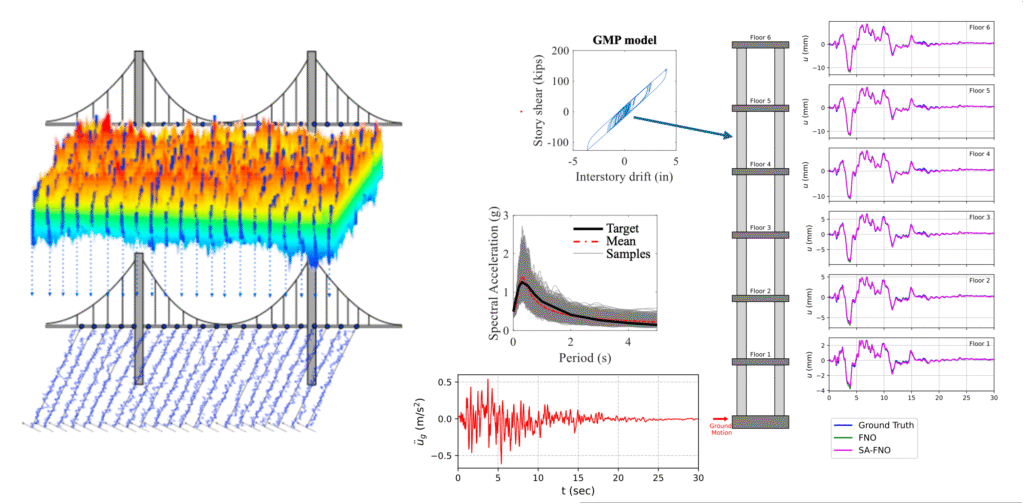
Natural hazards are often stochastic in nature, driven by extreme fluctuations in the randomly occurring forces of nature. SURG uses probabilistic methods to model these hazards to assess their impact on critical infrastructure systems. The following are representative papers:
- D. Giovanis, A. Taflanidis, and M. D. Shields. “Accelerating uncertainty quantification in incremental dynamic analysis using dimension reduction-based surrogate modeling”. Bulletin of Earthquake Engineering. 23 (2025), pp. 391–410. [DOI]
- M. Ojeda-Tuz, M. Chauhan, P. Fernandez-Caban, R. Catarelli, M. D. Shields, and K. Gurley. “Modulating higher-order statistics of turbulent boundary layer wind fields using randomized grid roughness”. Journal of Wind Engineering and Industrial Aerodynamics. 23 (2025), pp. 391–410. DOI: 10.1016/j.jweia.2025.106042.
- L. Vandanapu and M. D. Shields. “Simulation of non-Gaussian wind field as a 3rd-order stochastic wave”. Reliability Engineering and Systems Safety. 245 (2024), p. 109960. [DOI]
- H. Zhou, G. Deodatis, M. D. Shields, and B. A. Benowitz. “Simulation of wind velocity time histories on long span structures modeled as non-Gaussian stochastic waves”. Probabilistic Engineering Mechanics. 59 (2020), p. 103016. [DOI]
- M. D. Shields. “Simulation of spatially correlated nonstationary response spectrum–compatible ground motion time histories”. Journal of Engineering Mechanics. 141.6 (2015), p. 04014161. [DOI]
Materials Modeling
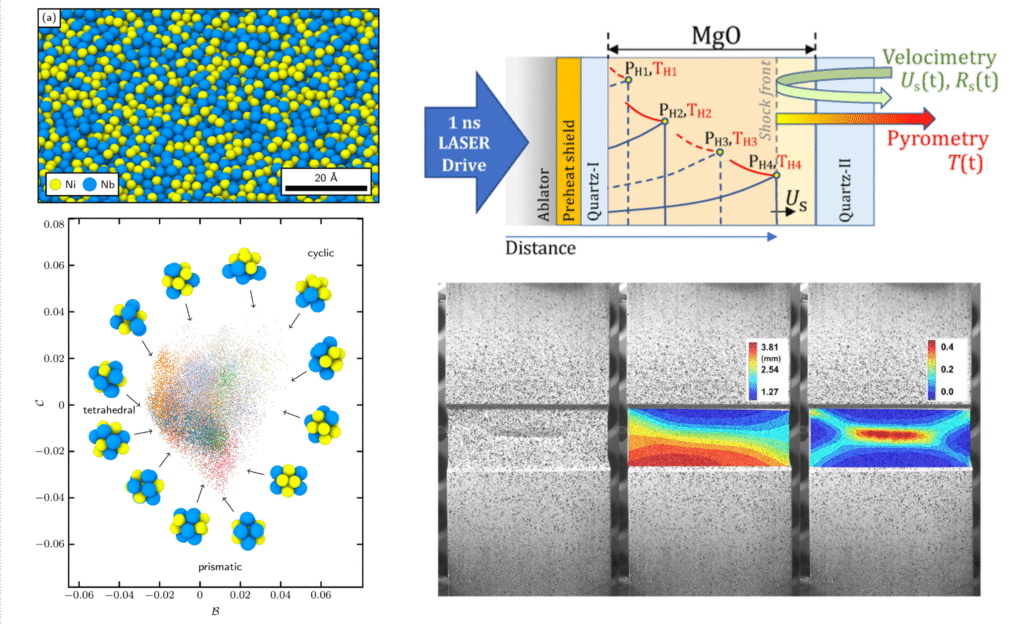
Materials modeling at length scales ranging from atomistic to structural scales requires modeling the stochastic nature of the material structure and its properties. Our group has worked on materials modeling at all scales and for diverse materials classes from ceramics and glasses to structural metals and concrete under extreme conditions. The following are representative papers:
- T. J. Hardin, M. Chandross, R. Meena, S. Fajardo, D.G. Giovanis, Y. Kevrekidis, M. L. Falk, and M. D. Shields. “Revealing the Hidden Structure of Disordered Materials by Parameterizing their Local Structural Manifold”. Nature Communications. 15 (2024), p. 4424. [DOI]
- H. Sharma, J. A. Gaffney, D. Tsapetis, and M. D. Shields. “Learning thermodynamically constrained equations of state with uncertainty”. APL Machine Learning. 2 (2024), p. 016102. [DOI]
- Z. Ye, R. F. Smith, M. Millot, M. Sims, D. Tsapetis, M. D. Shields, S. Singh, A. Hari, and J. K. Wicks. “Shock equation of state experiments in MgO up to 1.5 TPa and the effects of optical depth on temperature determination”. Journal of Applied Physics 136 (2024), p. 105904. [DOI]
- S. L. N. Dhulipala et al. “Accelerated Statistical Failure Analysis of Multifidelity TRISO Fuel Models”. Journal of Nuclear Materials. 563 (2022), p. 153604. [DOI]
- A. Bhaduri, C. S. Meyer, J. W. Gillespie Jr, B. Z. Haque, M. D. Shields, and L. Graham-Brady. “Probabilistic modeling of discrete structural response with application to composite plate penetration models”. Journal of Engineering Mechanics. 147.11 (2021), p. 04021087. [DOI]
- K. Kontolati, D. Alix-Williams, N. M. Boffi, M. L. Falk, C. H. Rycroft, and M. D. Shields. “Manifold learning for coarse-graining atomistic simulations: Application to amorphous solids”. Acta Materialia. 215 (2021), p. 117008. [DOI]
- J. Zhang, M. D. Shields, and S. Termaath. “Probabilistic modeling and prediction of out-of-plane unidirectional composite lamina properties”. Mechanics of Advanced Materials and Structures. (2020). [DOI]
- B.S. Aakash, S. Bi, M. D. Shields, and S. Gaitanaros. “On the high-temperature crushing of metal foams”. International Journal of Solids and Structures. 174–175 (2019), pp. 18–27. [DOI]
- B.S. Aakash, JP. Connors, and M. D. Shields. “Variability in the thermo-mechanical behavior of structural aluminum”. Thin-Walled Structures. 144 (2019), p. 106122. [DOI]
- A. R. Hinkle, C. H. Rycroft, M. D. Shields, and M. L. Falk. “Coarse-graining atomistic simulations of plastically deforming amorphous solids”. Physical Review E. 95 (2017), p. 053001. [DOI]
- P. B. Woelke, M. D. Shields, and J. W. Hutchinson. “Cohesive zone modeling and calibration for mode I tearing of large ductile plates”. Engineering Fracture Mechanics. 147 (2015), pp. 293–305. [DOI]
- P. B. Woelke, M. P. Rutner, M. D. Shields, C. Rans, and R. Alderliesten. “Finite element modeling of fatigue in fiber–metal laminates”. AIAA Journal. 53.8 (2015), pp. 2228–2236. [DOI]
- P. B. Woelke, M. D. Shields, N. N. Abboud, and J. W. Hutchinson. “Simulations of ductile fracture in an idealized ship grounding scenario using phenomenological damage and cohesive zone models”. Computational Materials Science. 80 (2013), pp. 79–95. [DOI]
Stochastic Process Modeling
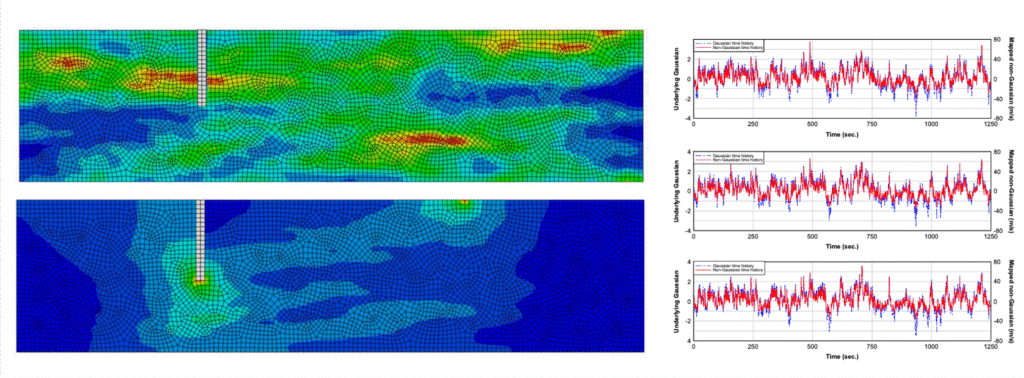
Numerous physical phenomena from wind velocity and seismic acceleration histories to material properties are modeled as stochastic processes. SURG focuses on modeling stochastic processes that have characteristics that are difficult to model such as non-Gaussian probability distributions and non-stationarity or statistical heterogeneity. The following are representative papers:
- G. Deodatis and M. D. Shields. “The Spectral Representation Method: A Framework for Simulation of Stochastic Processes, Fields, and Waves”. Reliability Engineering and System Safety. 254 (2025), p. 110522. [DOI]
- P.-P. Fang, Y. Liu, and M. D. Shields. “Direct simulation algorithms for a class of normal and lognormal random fields with applications in modelling material properties”. Journal of Engineering Mechanics. 148 (2022), p. 04021146. [DOI]
- L. Vandanapu and M. D. Shields. “Simulation of non-stationary and non-Gaussian random processes by 3rd-order Spectral Representation Method: Theory and POD implementation”. Mechanical Systems and Signal Processing. 178 (2022), p. 109150. [DOI]
- L. Vandanapu and M. D. Shields. “3rd-order Spectral Representation Method: Simulation of multi-dimensional random fields and ergodic multi-variate random processes with fast Fourier transform implementation”. Probabilistic Engineering Mechanics. (2021). [DOI]
- Y. Liu and M. D. Shields. “A direct simulation method and lower-bound estimation for a class of gamma random fields with applications in modelling material properties”. Probabilistic Engineering Mechanics. 47 (2017), pp. 16–25. [DOI]
- M. D. Shields and H. Kim. “Simulation of higher-order stochastic processes by spectral representation”. Probabilistic Engineering Mechanics. 47 (2017), pp. 1–15. [DOI]
- B. A. Benowitz, M. D. Shields, and G. Deodatis. “Determining evolutionary spectra from non-stationary autocorrelation functions”. Probabilistic Engineering Mechanics. 41 (2015), pp. 73–88. [DOI]
- H. Kim and M. D. Shields. “Modeling strongly non-Gaussian non-stationary stochastic processes using the Iterative Translation Approximation Method and Karhunen–Loeve expansion”. Computers & Structures. 161 (2015), pp. 31–42. [DOI]
- M. D. Shields and G. Deodatis. “A simple and efficient methodology to approximate a general non-Gaussian stationary stochastic vector process by a translation process with applications in wind velocity simulation”. Probabilistic Engineering Mechanics. 31 (2013), pp. 19–29. [DOI]
- M. D. Shields and G. Deodatis. “Estimation of evolutionary spectra for simulation of non-stationary and non-Gaussian stochastic processes”. Computers & Structures. 126 (2013), pp. 149–163. [DOI]
- M. D. Shields, G. Deodatis, and P. Bocchini. “A simple and efficient methodology to approximate a general non-Gaussian stationary stochastic process by a translation process”. Probabilistic Engineering Mechanics. 26.4 (2011), pp. 511–519. [DOI]
Bio-Mechanics
Recently, our group has become more interested in the mechanics of biological materials under uncertainty. This involves the modeling of soft materials such as human brain tissue under extreme conditions such as those causing traumatic brain injury. The following are representative papers:
- K. Upadhyay et al. “Effect of human head shape on the risk of traumatic brain injury: a gaussian process regression-based machine learning approach”. Military medicine. (2024), usae199. [DOI]
- K. Upadhyay et al. “Data-driven Uncertainty Quantification for Human Head Models”. Computer Methods in Applied Mechanics and Engineering. 398 (2022), p. 115108. [DOI]
Datasets
We believe in making data, models, and code available whenever possible. Many publications contain direct links to code for to proposed methods and/or data generated using the code. Moreover, the group publishes our general methodology through the open-source UQpy software. Below are links to public data sets generated by the group:
- M. Ojeda-Tuz, K. Gurley, M. D. Shields, M. Chauhan, and R. Catarelli. Pressure coefficients on a simple geometry Bluff body generated by a randomized terrain in a Boundary Layer Wind Tunnel. 2025. [DOI]
- M. Ojeda-Tuz, K. Gurley, M. D. Shields, M. Chauhan, R. Catarelli, and F. Masters. Wind Profiles in a Boundary Layer Wind Tunnel based on Different Approach Terrain Configurations. 2023. [DOI]
- M. D. Shields. Stress-strain data for aluminum 6061-T651 from 9 lots at 6 temperatures under uniaxial and plain strain tension. 2019. [DOI]

